What is a Camera Matrix?

The camera matrix is one of the most important concepts in computer vision. It determines the relationship between 3D points in the world and their 2D projections in an image.

Scroll for more

The Camera Projection Equation

The camera projection equation is the transformation which maps 3D points to the 2D image plane. It is a linear transformation which can be written as:

Where x is the 3D point, y is the 2D point, and P is the camera matrix. The tilde over the points x and y indicate that these are in homogeneous coordinates. What this means, and the reason we do this will become clear later.

Our camera matrix P is itself a product of two components, the intrinsic matrix K, and the extrinsic matrix [R|T].

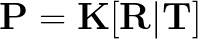
First let's look more closely at the extrinsic matrix, [R|T].

Scroll for more

Extrinsics: World to Camera

The extrinsic matrix maps points from the original coordinate system, where x y and z are measured in a world frame of reference, to a system where their x y and z are measured in the camera frame of reference.

Converting the points from one reference frame to another involves two steps: translation and rotation.

Scroll for more

Extrinsics: Translation

Suppose that we have a point in the world, x, and we wish to know its position in the frame of reference of the camera xₖ. By simple vector addition, the position of the point in camera coordinates is the sum of the position of the origin in the camera coordinates oₖ and the vector connecting the origin to the point in the same coordinate frame.

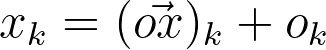
The first component of this sum, oₖ, the position of the origin in camera coordinates, is the translation vector T. This vector is the first part of the extrinsic matrix. See how changing the value of T changes the position of the point in camera coordinates.

Scroll for more

Extrinsics: Rotation

So are we done? We simply take the translation vector and add it to the point in world coordinates to give the point in camera coordinates?

Not so fast. Recall that we are working in the camera coordinate system, whereas the location of x is given in world coordinates. We still need to rotate the point into the camera coordinate system. However, this is fairly simple. We simply find the rotation matrix R which rotates points from the world coordinate system to camera coordinates.

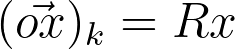
Practically speaking, this is given by the orientation of the world axes when viewed in the camera coordinate system. If you could measure the vectors of the world axes x, y, and z in the camera coordinate system, you would form this rotation matrix with these vectors as columns.

Scroll for more

Extrinsics: Rotation

Adjust the pitch, roll and yaw of the camera to see how the position, and the image, changes.

Scroll for more

Extrinsics: Forming the Matrix

Now we have all the pieces we need. To find the location of a point in the camera coordinate system, we rotate a given point with a rotation matrix R, and then translate it with the translation vector T:

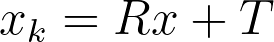
We can write this more compactly via the extrinsic matrix [R|T]:

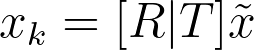
Where the tilde over the points indicates that we have appended [1] to the end of the vector. You can verify that this is the same as the previous equation.

Scroll for more

Extrinsics: Practical Considerations

However, in reality we typically set the location and rotation of the camera in the world coordinate system, not the other way around.

Fortunately, the two matrices are separated by a simple inverse operation. Given the location and rotation of the camera in the world coordinate system, the location and rotation in the camera frame is given by:

Scroll for more

Extrinsics: Sandbox

Try adjusting the camera rotation and translation to see how the extrinsics change.

Scroll for more

Intrinsics

The intrinsic matrix, K, is the second half of the camera matrix. We now have the location of any given point in the camera coordinate system. Now we need to project this point onto the image plane.

Projection is the process of converting rays to points. Any point which lies on a ray emanating from the camera center will project to the point of intersection of the ray with the image plane. The equation for this projection operation is given by the equation of a ray:

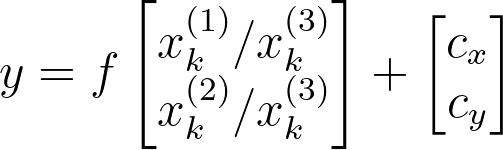
Scroll for more

Intrinsics: Focal Length

The first component to address in this equation is the focal length. The focal length defines the distance from the camera center to the image plane.

A more intuitive way to think about the focal length of the camera is that it defines the field of view of the camera. If the focal length is large, then a smaller solid angle is captured on the image plane, resulting in a smaller field of view.

Scroll for more

Intrinsics: Camera Center

The other part of the projection equation is the camera center. This is the point on the image plane which is the projection of the camera center.

If we move the camera center to the left, all points will also appear to move to the left on the image plane. Similarly, if we move the camera center up, points will appear to move up on the image plane.

Scroll for more

Intrinsics: Putting it Together

We can write the projection equation more compactly with the intrinsic matrix K:

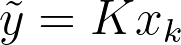
The equation yields the homogeneous point on the image plane, y, given the 3D point in camera coordinates, xₖ.

Note the tilde, again indicating that y is in homogeneous coordinates. To map back to inhomogeneous coordinates, we can simply divide the first two values by the third. You can verify this is the same as the projection equation described earlier.

Scroll for more